Top MCQs on Tree Traversal with Interview Question and Answers | DSA Quiz
Question 1
Following function is supposed to calculate the maximum depth or height of a Binary tree -- the number of nodes along the longest path from the root node down to the farthest leaf node.
C
What should be the values of X and Y so that the function works correctly?
int maxDepth(struct node* node)
{
if (node==NULL)
return 0;
else
{
/* compute the depth of each subtree */
int lDepth = maxDepth(node->left);
int rDepth = maxDepth(node->right);
/* use the larger one */
if (lDepth > rDepth)
return X;
else return Y;
}
}
Question 2
What is common in three different types of traversals (Inorder, Preorder and Postorder)?
Question 3
The inorder and preorder traversal of a binary tree are d b e a f c g and a b d e c f g, respectively. The postorder traversal of the binary tree is:
Question 4
What does the following function do for a given binary tree?
C
int fun(struct node *root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 0;
return 1 + fun(root->left) + fun(root->right);
}
Question 5
Which of the following pairs of traversals is not sufficient to build a binary tree from the given traversals?
Question 6
Consider two binary operators \'[Tex]\\uparrow[/Tex] \' and \'[Tex]\\downarrow[/Tex]\' with the precedence of operator [Tex]\\downarrow[/Tex] being lower than that of the [Tex]\\uparrow[/Tex] operator. Operator [Tex]\\uparrow[/Tex] is right associative while operator [Tex]\\downarrow[/Tex] is left associative. Which one of the following represents the parse tree for expression (7 [Tex]\\downarrow[/Tex] 3 [Tex]\\uparrow[/Tex] 4 [Tex]\\uparrow[/Tex] 3 [Tex]\\downarrow[/Tex] 2)? (GATE CS 2011)
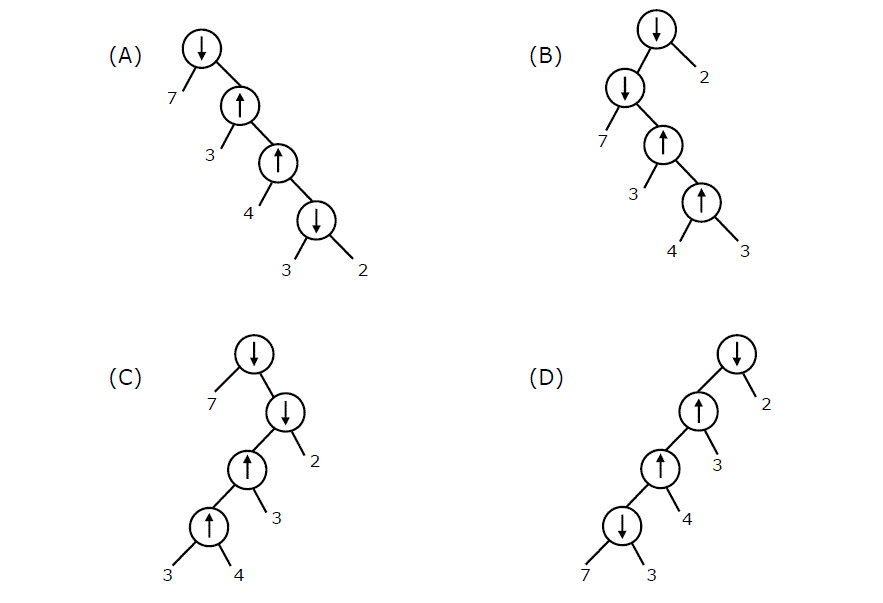
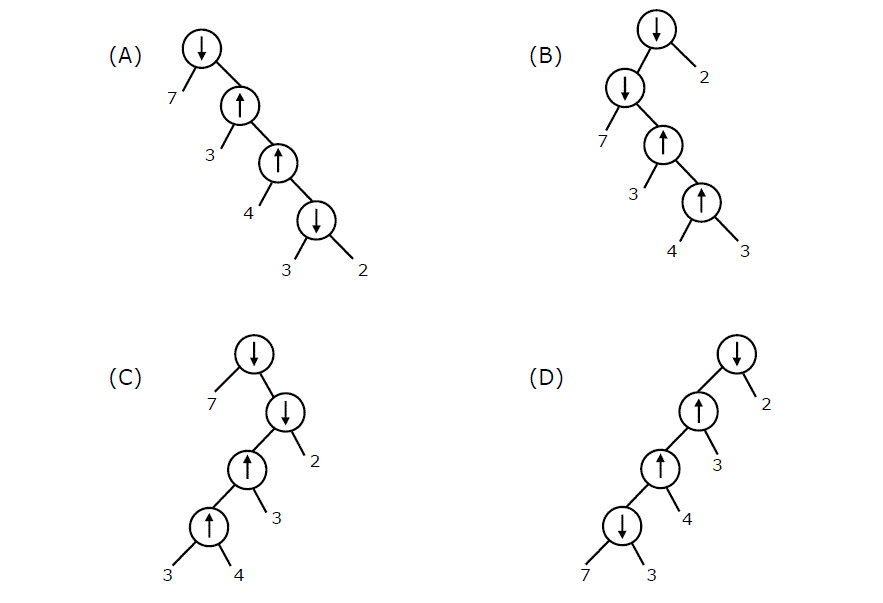
Question 10
Consider the following C program segment
c
The value returned by the function DoSomething when a pointer to the root of a non-empty tree is passed as argument is (GATE CS 2004)
struct CellNode
{
struct CelINode *leftchild;
int element;
struct CelINode *rightChild;
}
int Dosomething(struct CelINode *ptr)
{
int value = 0;
if (ptr != NULL)
{
if (ptr->leftChild != NULL)
value = 1 + DoSomething(ptr->leftChild);
if (ptr->rightChild != NULL)
value = max(value, 1 + DoSomething(ptr->rightChild));
}
return (value);
}
There are 42 questions to complete.
Last Updated :
Take a part in the ongoing discussion