Database Design(Normal Forms)

Question 1

For the relation R(ABCDEFGH) with FD's= {CH->G, A->BC, B->CHF, E->A, F->EG such that F+ is exactly the set of FDs that hold for R.} Consider the FDs given in above question. The relation R is

• in 1NF, but not in 2NF.

• in 2NF, but not in 3NF.

• in 3NF, but not in BCNF.

• in BCNF

Question 2

Which of the following is TRUE?

• Every relation in 3NF is also in BCNF
• A relation R is in 3NF if every non-prime attribute of R is fully functionally dependent on every key of R
• Every relation in BCNF is also in 3NF
• No relation can be in both BCNF and 3NF

Question 3

Consider a relational table with a single record for each registered student with the following attributes.

1. Registration_Num: Unique registration number
   of each registered student
2. UID: Unique identity number, unique at the 
   national level for each citizen
3. BankAccount_Num: Unique account number at
   the bank. A student can have multiple accounts
   or join accounts. This attribute stores the 
   primary account number.
4. Name: Name of the student
5. Hostel_Room: Room number of the hostel 

Which one of the following option is INCORRECT?

• BankAccount_Num is candidate key
• Registration_Num can be a primary key
• UID is candidate key if all students are from the same country
• If S is a superkey such that S∩UID is NULL then S∪UID is also a superkey

Question 4

Consider the following relational schema:

Suppliers(sid:integer, sname:string, city:string, street:string)
Parts(pid:integer, pname:string, color:string)
Catalog(sid:integer, pid:integer, cost:real)

Assume that, in the suppliers relation above, each supplier and each street within a city has a unique name, and (sname, city) forms a candidate key. No other functional dependencies are implied other than those implied by primary and candidate keys. Which one of the following is TRUE about the above schema?

• The schema is in BCNF
• The schema is in 3NF but not in BCNF
• The schema is in 2NF but not in 3NF
• The schema is not in 2NF

Question 5

Consider the following relational schemes for a library database: Book (Title, Author, Catalog_no, Publisher, Year, Price) Collection (Title, Author, Catalog_no) with in the following functional dependencies:

I. Title Author --> Catalog_no
II. Catalog_no --> Title, Author, Publisher, Year
III. Publisher Title Year --> Price 

Assume {Author, Title} is the key for both schemes. Which of the following statements is true?

• Both Book and Collection are in BCNF
• Both Book and Collection are in 3NF only
• Book is in 2NF and Collection is in 3NF
• Both Book and Collection are in 2NF only

Question 6

Consider the relation scheme R = {E, F, G, H, I, J, K, L, M, N} and the set of functional dependencies {{E, F} -> {G}, {F} -> {I, J}, {E, H} -> {K, L}, K -> {M}, L -> {N} on R. What is the key for R?

• {E, F}

• {E, F, H}

• {E, F, H, K, L}

• {E}

Question 7

Given the following two statements:

  S1: Every table with two single-valued 
      attributes is in 1NF, 2NF, 3NF and BCNF.

  S2: AB->C, D->E, E->C is a minimal cover for 
      the set of functional dependencies 
      AB->C, D->E, AB->E, E->C. 

Which one of the following is CORRECT?

• S1 is TRUE and S2 is FALSE.
• Both S1 and S2 are TRUE.
• S1 is FALSE and S2 is TRUE.
• Both S1 and S2 are FALSE.

Question 8

The maximum number of superkeys for the relation schema R(E,F,G,H) with E as the key is

• 5
• 6
• 7
• 8

Question 9

Given the STUDENTS relation as shown below. 

[caption width="800"]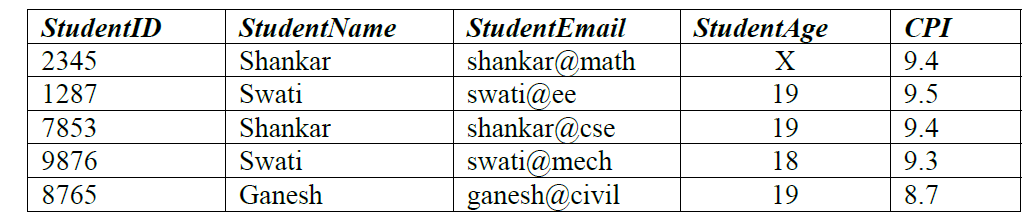 [/caption]

For (StudentName, StudentAge) to be the key for this instance, the value X should not be equal to

• 18

• 19

• 17

• 20

Question 10

Which one of the following statements about normal forms is FALSE?

• BCNF is stricter than 3NF
• Lossless, dependency-preserving decomposi­tion into 3NF is always possible
• Lossless, dependency-preserving decomposi­tion into BCNF is always possible
• Any relation with two attributes is in BCNF