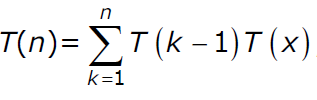GATE-CS-2003
Question 1
Consider the following C function.
float f(float x, int y)
{
float p, s; int i;
for (s=1, p=1, i=1; i < y; i ++)
{
p*= x/i;
s+=p;
}
return s;
}
For large values of y, the return value of the function f best approximates
Question 2
Assume the following C variable declaration
int *A [10], B[10][10];
Of the following expressions :
- A[2]
- A[2][3]
- B[1]
- B[2][3]
which will not give compile-time errors if used as left hand sides of assignment statements in a C program?
Question 3
Let P(E) denote the probability of the event E. Given P(A) = 1, P(B) = 1/2, the values of P(A | B) and P(B | A) respectively are
Question 4
Let A be a sequence of 8 distinct integers sorted in ascending order. How many distinct pairs of sequences, B and C are there such that (i) each is sorted in ascending order, (ii) B has 5 and C has 3 elements, and (iii) the result of merging B and C gives A?
Question 5
Question 6
Question 7
Consider the set ∑* of all strings over the alphabet ∑ = {0, 1}. ∑* with the concatenation operator for strings
Question 8
Let G be an arbitrary graph with n nodes and k components. If a vertex is removed from G, the number of components in the resultant graph must necessarily lie between
Question 9
Assuming all numbers are in 2\'s complement representation, which of the following numbers is divisible by 11111011?
Question 10
For a pipelined CPU with a single ALU, consider the following situations
1. The j + 1-st instruction uses the result of the j-th instruction
as an operand
2. The execution of a conditional jump instruction
3. The j-th and j + 1-st instructions require the ALU at the same
time
Which of the above can cause a hazard ?
There are 89 questions to complete.
Last Updated :
Take a part in the ongoing discussion