GATE-CS-2007
Question 1
Consider the following two statements about the function f(x)=|x|
P. f(x) is continuous for all real values of x Q. f(x) is differentiable for all real values of x
Which of the following is TRUE?
Question 2
Let S be a set of n elements. The number of ordered pairs in the largest and the smallest equivalence relations on S are:
Question 3
What is the maximum number of different Boolean functions involving n Boolean variables?
Question 4
Let G be the non-planar graph with the minimum possible number of edges. Then G has
Question 5
Consider the DAG with Consider V = {1, 2, 3, 4, 5, 6}, shown below. Which of the following is NOT a topological ordering?
[caption width="800"]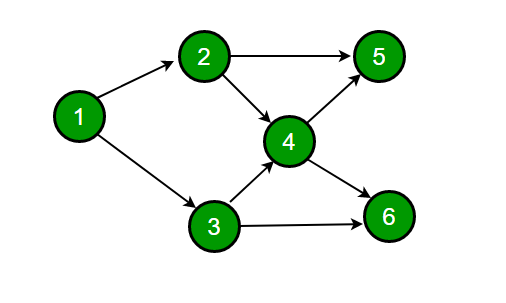 [/caption]
[/caption]Question 8
Question 9
Question 10
Consider a 4-way set associative cache consisting of 128 lines with a line size of 64 words. The CPU generates a 20-bit address of a word in main memory. The number of bits in the TAG, LINE and WORD fields arerespectively:
There are 85 questions to complete.