What Boolean function does the circuit below realize ?
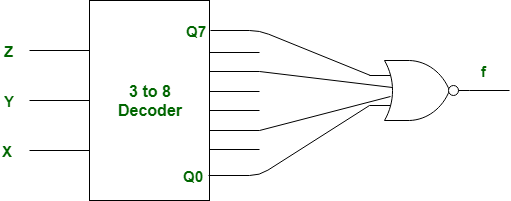
Question 9-Explanation:
There 0, 2, 5, 7 are enable input in given decoder.
Therefore, given K-Map should be as following:

So, output of above K-Map is,
= xz + x\'z\'
= (x⊙z)
= x (ex-nor) z
But, there given gate is NOR instead of OR, therefore above output will be negatated.
So, output function f is,
f = (xz + x\'z\')\'
= x\'z + xz\'
= (x⊕z)
= x (xor) z
So, option (B) is correct.
This explanation is contributed by
Deep Shah.