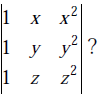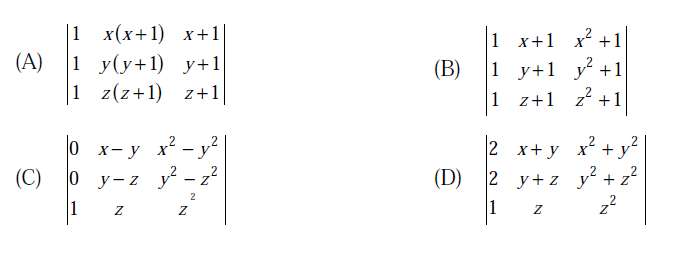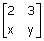Linear Algebra
Question 2
Question 3
Question 5
Consider a matrix [Tex]A = uv^T[/Tex] where [Tex]u = \\begin{pmatrix}
1\\\\
2
\\end{pmatrix}, v = \\begin{pmatrix}
1\\\\
1
\\end{pmatrix}[/Tex]. Note that [Tex]v^T[/Tex] denotes the transpose of v. The largest eigenvalue of A is ________ .
Note -This was Numerical Type question.
Question 7
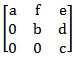
If the matrix A is such that
[caption width="800"] [/caption]
[/caption]
then the determinant of A is equal to
Question 8
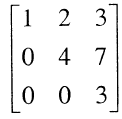
The product of the non-zero eigenvalues of the matrix
1 0 0 0 1 0 1 1 1 0 0 1 1 1 0 0 1 1 1 0 1 0 0 0 1
is ______
Question 10
There are 77 questions to complete.
Last Updated :
Take a part in the ongoing discussion