Rolle’s Mean Value Theorem

Rolle’s theorem one of the core theorem of calculus states that, for a differentiable function that attains equal values at two distinct points then it must have at least one fixed point somewhere between them where the first derivative of the function is zero.

What is Rolle’s Theorem?

Rolle’s Theorem or Rolle’s Mean Value Theorem is a fundamental theorem of calculus that states,

Rolle’s Theorem Statement

“A function f defined in the closed interval [a, b] in such a way that it satisfies the following condition:

1. f(x) is continuous in the closed interval a ≤ x ≤ b
2. f(x) is differentiable in the open interval a < x < b
3. f(a) = f(b)

Then, there exists at least one point ‘c’ in the open interval (a, b) such that:

f'(c) = 0

Geometric Interpretation of Rolle’s Theorem

We can visualize Rolle’s theorem from the figure(1) added below,

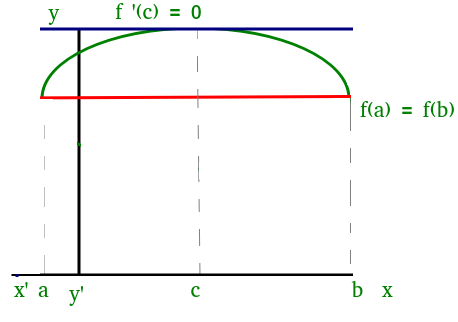
In the above figure the function satisfies all three conditions given above. So, we can apply Rolle’s theorem, according to which there exists at least one point ‘c’ such that:

f'(c) = 0

which means that there exists a point at which the slope of the tangent at that is equal to 0. We can easily see that at point ‘c’ slope is 0. Similarly, there could be more than one points at which slope of tangent at those points will be 0. Figure(2) added below is one of the example where exists more than one point satisfying Rolle’s theorem.

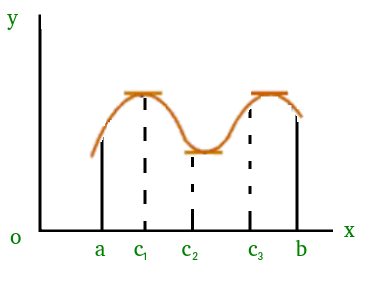
Examples on Rolle’s Theorem

Example 1: Verify Rolle’s theorem for function y = x² + 4, a = –1 and b = 1.

Solution:

Given function y = x² + 4, as it is a polynomial function, is continuous in [– 1, 1] and differentiable in (–1, 1). Also,

f(-1) = (-1)² + 4 = 1 + 4 = 5

f(1) = (1)² + 4 = 1 + 4 = 5

Thus, f(– 1) = f(1) = 5

Hence, the function f(x) satisfies all conditions of Rolle’s theorem.

Now, f'(x) = 2x

Rolle’s theorem states that there is a point c ∈ (– 1, 1) such that f′(c) = 0.

2c = 0

c = 0, where c = 0 ∈ (–1, 1)

Example 2: Verify Rolle’s theorem for function y = 2x + 8, a = –1 and b = 1.

Solution:

Given function y = 2x + 8, as it is a polynomial function, is continuous in [– 1, 1] and differentiable in (–1, 1). Also,

f(-1) = 2(-1) + 8 = -2 + 8 = -6

f(1) = 2(1) + 8 = 2 + 8 = 10

Thus, f(– 1) ≠ f(1)

Hence, Rolle’s theorem is not applicable.