Network Security
Question 1
Using public key cryptography, X adds a digital signature [Tex]\\sigma[/Tex] to message M, encrypts < M, [Tex]\\sigma[/Tex] >, and sends it to Y, where it is decrypted. Which one of the following sequences of keys is used for the operations?
Question 2
In the RSA public key cryptosystem, the private and public keys are (e, n) and (d, n) respectively, where n = p*q and p and q are large primes. Besides, n is public and p and q are private. Let M be an integer such that 0 < M < n and f(n) = (p- 1)(q-1). Now consider the following equations.
I. M’= Me mod n
M = (M’)d mod n
II. ed ≡ 1 mod n
III. ed ≡ 1 mod f(n)
IV. M’= Me mod f(n)
M = (M’)d mod f(n)
Which of the above equations correctly represent RSA cryptosystem?
Question 3
Which of the following are used to generate a message digest by the network security protocols?
(P) RSA (Q) SHA-1 (R) DES (S) MD5
Question 4
A sender is employing public key cryptography to send a secret message to a receiver. Which one of the following statements is TRUE?
Question 5
Consider that B wants to send a message m that is digitally signed to A. Let the pair of private and public keys for A and B be denoted 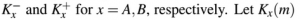 represent the operation of encrypting m with a key Kx and H(m) represent the message digest. Which one of the following indicates the CORRECT way of sending the message m along with the digital signature to A?
represent the operation of encrypting m with a key Kx and H(m) represent the message digest. Which one of the following indicates the CORRECT way of sending the message m along with the digital signature to A?
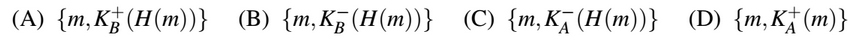
Question 6
Consider the following two statements:
i. A hash function (these are often used for computing digital signatures) is an injective function.
A. encryption technique such as DES performs a permutation on the elements of its input alphabet.
Which one of the following options is valid for the above two statements?
Question 7
Exponentiation is a heavily used operation in public key cryptography. Which of the following options is the tightest upper bound on the number of multiplications required to compute bn mod m,0≤b,n≤m ?
Question 8
The total number of keys required for a set of n individuals to be able to communicate with each other using secret key and public key crypto-systems, respectively are:
Question 9
S1- MD5 is vulnerable to the Birthday attack. S2- traceroute uses the "Destination port unreachable" ICMP error message. S3- 3DES is a type of Public Key Encryption Algorithm. S4- IPv6 has a 40-byte fixed header size(without Options fields).How many of the above statements are true?
Question 10
In a RSA cryptosystem, a participant A uses two prime numbers p=13 and q=11 to generate his public and private keys. If the public key of A is 37, then the private key of A is _____.
There are 40 questions to complete.
Last Updated :
Take a part in the ongoing discussion