Set Theory & Algebra
Question 1
A binary operation [Tex]\\oplus[/Tex] on a set of integers is defined as x [Tex]\\oplus[/Tex] y = x2 + y2. Which one of the following statements is TRUE about [Tex]\\oplus[/Tex]?
Question 2
Consider the set S = {1, ω, ω2}, where ω and w2 are cube roots of unity. If * denotes the multiplication operation, the structure (S, *) forms
Question 4
Consider the binary relation R = {(x, y), (x, z), (z, x), (z, y)} on the set {x, y, z}. Which one of the following is TRUE?
Question 5
For the composition table of a cyclic group shown below
[caption width="800"] [/caption]
[/caption]
Which one of the following choices is correct?
Question 7
Let S be a set of n elements. The number of ordered pairs in the largest and the smallest equivalence relations on S are:
Question 9
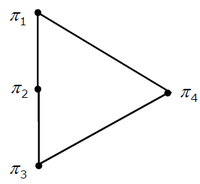
Consider the set S = (A, B, C, D}. Consider the following 4 partitions π1, π2, π3, π4 on S : π1 = {ABCD}' , π2 = {AB}' , {CD}' , π3 = {ABC}' , {D}' , π4 = A' , B' , C' , D'. Let P be the partial order on the set of partitions S' = {π1, π2, π3, π4} defined as follows : πi P πj if and only if πi refines πj. The poset diagram for (S', P ) is :
There are 121 questions to complete.
Last Updated :
Take a part in the ongoing discussion
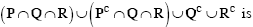
 [/caption]
[/caption]
 [/caption]
[/caption] [/caption]
[/caption]
-200.png) [/caption]
[/caption]
